Calculation of beam weight

Calculation of beam weight and the location of centroid.

Calculation of section properties

For each section at interval D_z the section properties are calculated: coordinates of centroid x_G and y_G, cross-sectional area A [mm²], moment of inertia I_x, I_y [mm⁴] and torsional moment of inertia I_t [mm⁴].

Beam Load

Input of beam load with dialog box:

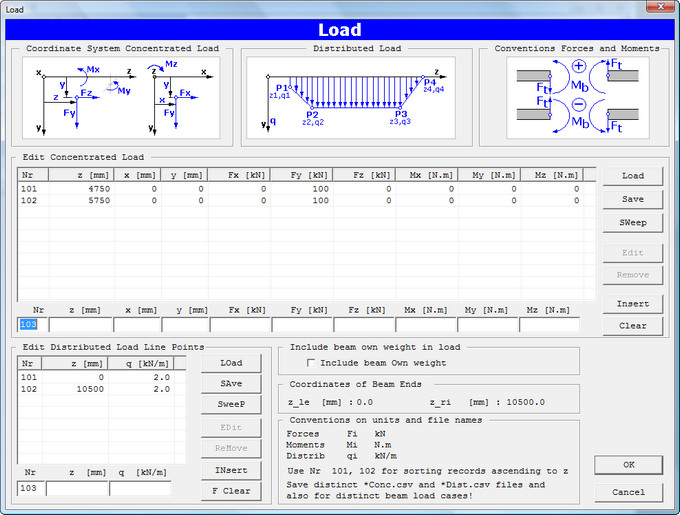
Input of concentrated load: the load is to define with coordinates of action point z, x, y [mm], forces F_x,y,z [kN] and moments M_x,y,z [N.m]. The coordinates x and y offer the possibility to define excentric loads. Input of distributed load by input of load line points z, q [kN/m]. The distributed load is converted to a discrete load acting in the centroid of the area under the load line. The user can check off if the own weight of the beam is to add to the load list. This option is disabled if the shaft cross section profile has not been defined, e.g. in the dimensioning problem.
The distributed load is described as a distirubuted force load caused by a mass rigidly connected to the beam and for the calculation of the natural frequency this force load is converted to mass.

Calculation of Reaction Forces in Supports

The reaction forces in supports A, B, C ... are determined in form R_x,y,z [kN]. For a cantilever beam the reaction moment M_x,y,z [N.m] is calculated.

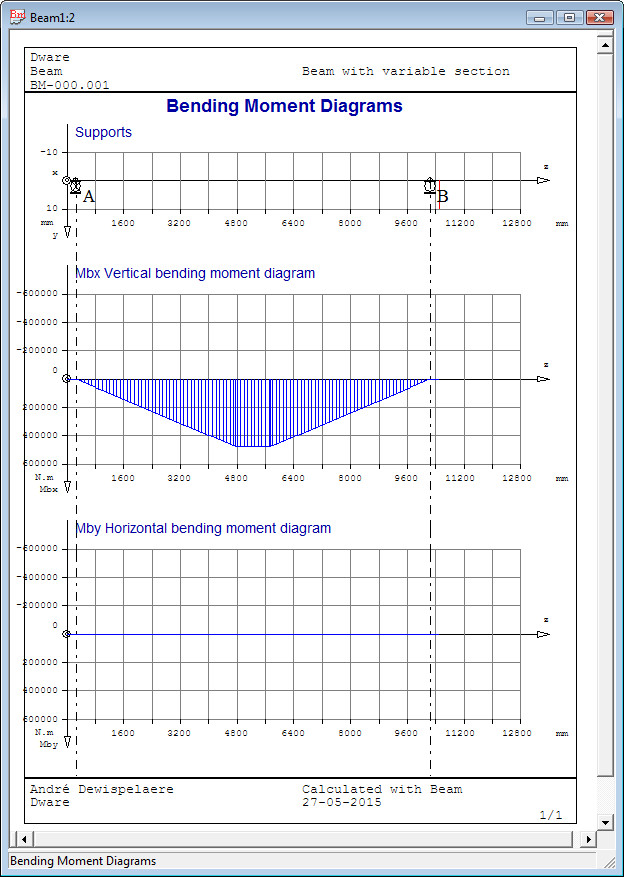
Calculation of Bending Moment Diagram

For each cross section in location coordinate z on distance D_z from each other are calculated: bending moments M_bx, M_by and torsional moment M_z [N.m] and axial force F_z [kN] if present.
The calculation records are displayed on the screen in a table. Graphical representation in a bending moment diagram, as in figure underneath:

Calculation of Transverse Forces

For each calculation point of the moment diagram, the transverse forces T_x, T_y [kN] and normal force F_z [kN] are calculated. Graphic representation in a transverse force diagram.

Go to next web page for stress and deflection calculation.