Worm Gear Pair Geometry Parameters
A worm gear pair is defined by a standardised theoretical basic rack profile and 7 independent geometric quantities:
|
1 |
Module |
mx or mn |
|
2 |
Number of starts of worm |
z1 |
|
3 |
Number of teeth of wheel |
z2 |
|
4 |
One of the following quantities |
da1, d1, q, γ |
|
5 |
Center distance |
a |
|
6 |
Worm length |
b1 |
|
7 |
Face width wheel |
b2 |
Input with following dialog box:
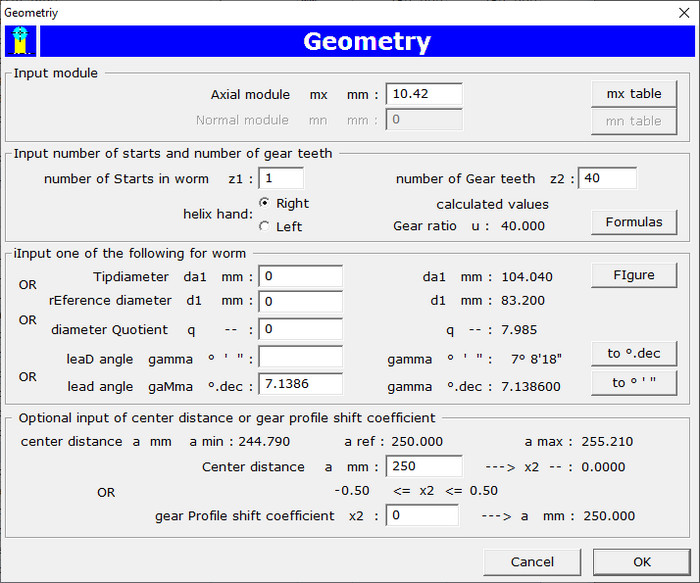
Input of a parameter or change of a parameter, followed by pressing the Tab key, triggers a calculation with actual input: the user can
see the effect of latest input.
Note that for the worm there is a choice for input of one independent quantity out of the following:
|
Tip diameter worm |
da1 |
|
Reference diameter worm |
d1 |
|
Diameter quotient |
q |
|
Lead angle |
γ |
Input of a quantity as independent and press the Tab key to calculate the others as dependent quantities.
The lead angle γ can be entered expressed in sexagesimal or in decimal degrees.
Input of center distance a is optional, on no entry the center distance is considered as dependent quantity.
Alternatively, the profile shift coefficient for wormwheel x2 can be entered, the center distance is then
considered as dependent quantity. The application calculates the minimum and maximum applicable center distances, while keeping the
profile shift coefficients in range. The minimum and maximum profile shift coefficients in function of the flank form are displayed
in the dialog box.
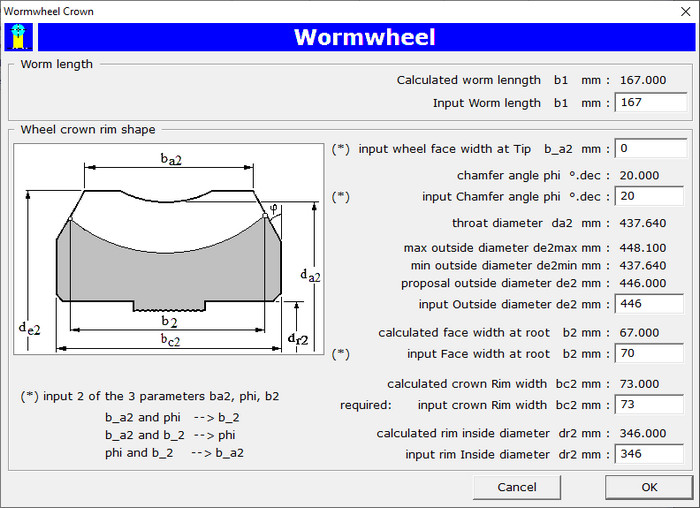
Still required input: face width at root of wormwheel b2 and crown width of wormwheel bc2
and some other design dimensions for the wormwheel crown. This is all done as shown in the following dialog box:
Mean normal backlash and backlash tolerance
The application allows the backlash to be apportioned over the worm with a scale from 0 to 100 %. Selection is done
by means of a trackbar. The rest percentage is then apportioned to the wormwheel.
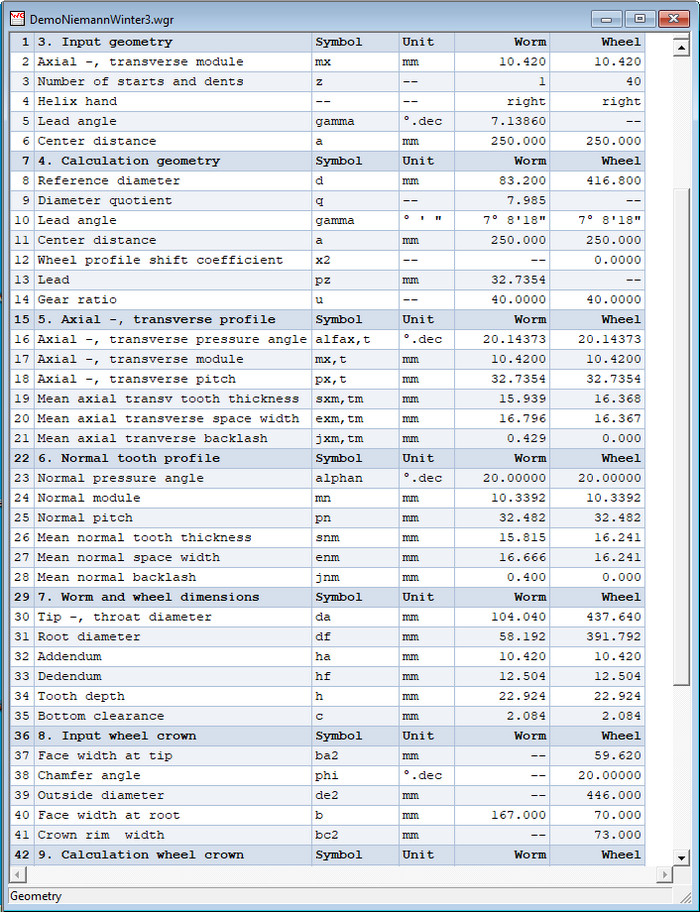
Results of geometry calculation in table form looks like:
Click here on Calculation Report Geometry to open it with your browser in a blank page.
Go to next web page for worm gear forces.